Álgebra Grado 9-1

Semana 11-13 (del 30 de junio al 17 de julio 2020)

finalización de semestre

Funciones Matemáticas

Hola chicos, ya estamos en la recta final del primer semestre del año escolar, ha sido todo un reto manejar esta nueva forma de aprender, pero se que la mayoría ha estado pendiente y haciendo un gran esfuerzo, los felicito por eso.

Vamos a continuar con el tema de funciones, hasta el mes pasado trabajamos un primer acercamiento a la noción de función, se establecio que una función es una relación matemática donde cada elemento del conjunto de partida se relaciona con un solo elemento del conjunto de llegada, los elementos del conjunto de partida le llamamos DOMINIO y a los elementos del conjunto de llegada que forman pareja con los elementos del dominio, se les llamó imagenes simbolizado como f(x) y son los elementos del RANGO.

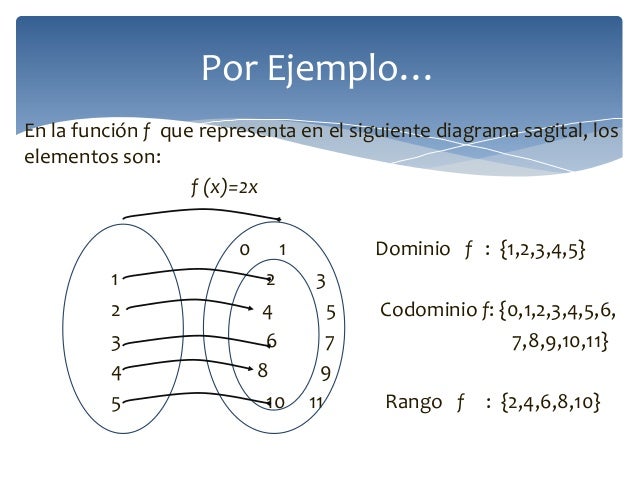
vimos que las funciones pueden representarse a través de diagramas sagitales como el anterior, también como un conjunto de pares ordenados, como gráficas en el plano cartesiano, o en lenguaje algebraico como una expresión algebraica o en lenguaje escrito u oral.

Por ejemplo, la función definida para el conjunto de los números enteros, es decir que su dominio son los número enteros, de la forma algebraica f(x)= 2x puede representarse en diagrama sagital como se mostró en la ilustración anterior, pero también podemos escribir las parejas ordenadas así:

(1, 2); (2,4); (3, 6); (4,8); (5,10); (6, 12), (7, 14)....

¿cuántas parejas ordenas se pueden formar? 

exacto, infinitas y no solo con imágenes positivas, pues el dominio es el conjunto de los números enteros que también esta conformado por número negativos así que podemos formar parejas ordenadas como:

(-1, -2); (-2, -4),...

la expresión f(x)= 2x representa la función descrita como "el doble de x" para todo valor de x que pertenezca al conjunto de los números enteros. y podemos representar esta función en el plano cartesiano, si ubicamos las parejas ordenas en él.

como puedes observar en la representación en el plano cartesiano, no se unen los puntos con una línea, pues como el dominio son los números enteros, solo podemos señalar dichos puntos. Si por el contrario el dominio corresponde al conjunto de los números reales (recuerda que los números reales esta formado por todos los números racionales e irracionales juntos, llenando la recta completamente) en ese caso si debemos unir los puntos con una línea.

Por ejemplo, sea la función f(x)= 3x+1, definida para el conjunto de los números reales, representa la función en el plano cartesiano y en lenguaje escrito en lengua natural, es decir, describe la función con palabras.

solución: primero obtengamos algunas parejas ordenadas para ubicarlas en el plano cartesiano, para esto debemos escoger valores para x y reemplazarlos en la función f(x), luego al obtener la imagen, es decir el resultado que tomará el valor de y, formamos el punto. Vamos a darles a x los valores de -2, -1.5, 0, 3/4 y 3 (pueden ser infinitos los valores numéricos ya que el conjunto de los números reales es infinito), luego reemplazamos en la expresión algebraica de la función, así:

f(x)=f(-2)= 3(-2)+1= -6+1= -5

f(x)=f(-1.5)= 3(-1.5)+1= -3.5

f(x)=f(3/4)=3(3/4)+1=9/4+1=9/4+4/4=13/4

f(x)=f(3)=3(3)+1=9+1=10

En el caso del número racional fraccionario, recuerda como hacer operaciones entre fracciones.

Ahora formemos las parejas ordenadas (x, y):

(-2, -5); (-1.5, -3.5); (3/4, 13/4); (3, 10) 

y representemos en el plano cartesiano, recuerda que como el dominio es el conjunto de los números reales y estos cubren la recta numérica totalmente, podemos trazar una línea para unir los puntos.

y podemos describir la función f(x) con lenguaje natural de la siguiente manera.

"Para cada elemento del conjunto de los números reales, existe una imagen que corresponde al triple del valor numérico del elemento aumentado en una unidad."

Recuerda tomar nota de todo lo visto hasta este momento, en tu cuaderno, como evidencia de actividad académica y para que puedas repasar. Con ayuda de los ejemplos ilustrados puedes realizar la actividad evaluativa dada a continuación:

Actividad Evaluativa

Dadas las funciones matemáticas en su forma algebraica, representarlas en el plano cartesiano y describirlas de manera escrita. Cada función está definida en el conjunto de los número reales, completa la tabla de valores en cada caso, escribe las parejas ordenadas que se forman y representa en el plano cartesiano. Cuando termines, toma fotos o escanea tu actividad y envialas al correo electrónico profeagl@gmail.com recuerda marcar el correo con tu nombre y apellido. Tienes plazo hasta el 17 de julio que se cierra el semestre.

________________________________________________________________

Semana 7-10 (del 1 al 26 de junio de 2020)

RELACIONES Y FUNCIONES MATEMÁTICAS

Hola chicos, espero se encuentren bien. Durante esta clases vamos a estudiar uno de los conceptos más importantes de la matemáticas y a partir del cual centraremos nuestro aprendizaje el resto del año escolar: Las funciones matemáticas.

Pero antes debemos identificar otro concepto importante, las relaciones matemáticas. LLamamos relación a toda correspondencia que se establece entre dos conjuntos, el primer conjunto se llama conjunto de partida y el segundo se llama conjunto de llegada. La relación matemática es un subconjunto del producto cartesiano que se establece entre ambos conjuntos. Por ejemplo:

Como puedes observar, a los elementos del conjunto de partida se les denomina Dominio de la relación, y al conjunto de elementos que son pareja de los elementos del dominio se les denomina Rango de la relación.

Vamos a observar algunos ejemplos de relaciones representadas en diagramas sagitales, trata de identificar el dominio y el rango de cada una

Escribe en tu cuaderno el dominio y el rango de cada relación, además, representalos en el plano cartesiano, en notación de conjunto y en forma algebraica.

FUNCIONES

Las funciones matemáticas, son un tipo especial de relación matemática, donde se deben cumplir dos condiciones:

1. Todo elemento del dominio debe tener imagen, es decir, debe tener una pareja en el conjunto de llegada.
2. Todo elemento del dominio debe tener UNA SOLA imagen.

Observa los siguientes ejemplos donde se muestran relaciones matemáticas, algunas son funciones y otras no:

Si observas, las relaciones 1, 3 y 6 son funciones porque cumplen las condiciones: todos los elementos del dominio tienen pareja y además tienen solo una pareja.

Por otro lado, las relaciones 2, 4 y 5 fallan en alguna de estas condiciones, por ejemplo en la relación 2, el elemento 4 del dominio no tiene pareja; en la relación 5, el elemento 1 tiene más de una pareja y en la relación 4, el elemento 5 no tiene pareja y además el elemento 4 tiene más de una pareja.

RECUERDA:

Cuando tenemos un punto de parejas cartesianas de la forma (x,y), recuerda que x es el elemento que pertenece al dominio, y es el elemento que pertenece al rango, además se escribe que y es la imagen de x de la siguiente manera:

f(x)= y

Por ejemplo, cuando vemos escrito f(2)= 5, significa que 5 es la imagen de 2, o 5 es la pareja de 2 a través de la función f y el punto que se forma para ubicarlo en el plano o en un diagrama sagital es (2, 5).

Como otra manera de representar las funciones son las expresiones algebraicas, podemos extraer de ellas algunos elementos del dominio y del rango. Pero para ello debemos tener en cuenta cuales elementos pueden ser parte del dominio, es decir, para que elementos del dominio el rango esta definido a través de la función. 

Por ejemplo, si tenemos la función f(x)= 2x+1, podemos analizar que para todo valor de x, existe un valor de f(x), puesto que la multiplicación y la suma que aparecen como operaciones en la expresión algebraica son operaciones bien definidas para todos los números reales. Así podemos escoger para x los valores que queramos:

f(2)= 5, porque al reemplazar x=2 en la función se tiene 2(2)+1=4+1=5

f(-3)=-5, porque al reemplazar x=-5 en la función se tiene 2(-3)+1=-6+1=-5

f(0)= 1, porque al reemplazar x=0 en la función se tiene 2(0)+1=0+1=1

Vamos a complementar la clase de la primera parte del estudio de relaciones y funciones con algunos video de apoyo y al finalizar se propone una actividad que tiene dos partes.

Video 1

Video 2

Video 3

Video 4

Tarea: Esta parte de la tarea debes desarrollarla en el cuaderno, teniendo en cuenta todo lo expuesto en esta clase (por eso espero que hayas tomado nota), después debes tomarle foto o escanear (es mejor) y enviar al correo profeagl@gmail.com

1. Para cada uno de los siguientes diagramas sagitales, determina cuales relaciones son funciones y cuales no lo son, explica en cada caso.
2. Para el caso de las relaciones que si son funciones del punto anterior, representalas en notación de conjunto, en el plano cartesiano y en expresión algebraica.
3. Consulta los problemas que pueden presentarse en el dominio de una función, copiar en el cuaderno y realizar 3 ejemplos de cada tipo de problemas.

ACTIVIDAD EVALUATIVA

La segunda parte de la tarea es desarrollar el siguiente cuestionario, recuerda que al finalizar debes dar clic en enviar.

                                                                                                                   

Semana 5-6 (del 18 al 29 de mayo de 2020)

Multiplicación de Expresiones Radicales con diferente índice (heterogéneas)

Hola a todos, espero se encuentren muy bien. Teniendo en cuenta la densidad de actividades de todas las materias y a petición de padres de familia y estudiantes, las clases y actividades para mi área serán presentadas para dos semanas, así tendrás mas espacio para su desarrollo. Ahora sí continuemos donde quedamos la semana pasada.

En la clase anterior, aprendimos como multiplicar expresiones radicales de igual índice, es decir, expresiones de índice homogéneo. En esta clase veremos los procedimientos necesarios para multiplicar expresiones radicales de índices heterogéneos (diferentes) para eso necesitamos calcular el mínimo común múltiplo entre los índices y así homogeneizarlos, de esta manera se convertirán en radicales con el mismo indice y los multiplicaremos como aprendimos la semana 3 y 4.

Recuerda que es muy importante conocer y utilizar correctamente, las propiedades de los exponentes y los radicales, puedes copiar las tablas de propiedades vistas en la semana 3 y 4, en cartulina y tenerlas a la mano en el desarrollo de la actividad, es algo muy útil.

Veamos a continuación un video de mi canal youtube con varios ejemplos de los procedimientos que debemos realizar para multiplicar expresiones radicales con índices diferentes, luego te presentaré dos videos escogidos de los canales de youtube de otros profes como apoyo para que puedas fortalecer los procesos.

Recuerda tomar nota de los aspectos más importantes y los ejemplos de esta clase en tu cuaderno, como evidencia de actividad académica y para tenerlo como recurso de consulta y estudio.

Vídeo 1: Multiplicación y simplificación de expresiones radicales con diferente índice.

Vídeo 2: Otros ejemplos de apoyo

Vídeo 3: Más ejemplos

Actividad Evaluativa 3

Para esta semana debes desarrollar el siguiente taller en tu cuaderno ( todos menos el punto i)y tomarle foto o escanear (puedes descargar un app de escáner en tu celular así los archivos pesan menos y puedes cargarlos con mayor facilidad) debes enviar todas las fotos con el procedimiento y los resultados al correo electrónico profeagl@gmail.com debidamente marcado con nombres y apellidos completos

IMPORTANTE: no se reciben actividades por whatsApp, solo pueden ser enviados por correo electrónico a la dirección que se dijo anteriormente.

Semana 3 y 4 (del 4 al 15 de mayo de 2020)

Expresiones Radicales: propiedades y operaciones. Multiplicación

Hola, espero que estés súper bien y cuidándote en casita, además listo para iniciar de nuevo nuestras actividades académicas luego de este forzoso receso. Vamos a continuar con el proceso de aprendizaje de expresiones radicales, sus propiedades y operaciones en su representación algebraica. 

Esta semana 2 vamos a concentrarnos en dos operaciones: la multiplicación. Pero primero debemos recordar las propiedades tanto de la potencia como de la radicación. Observa y consigna en tu cuaderno el siguiente cuadro:

 Propiedades de la Potenciación (tabla 1)

Recuerda que los parámetros a y b, son elementos del conjunto de los números Reales de acuerdo a lo especificado en cada propiedad.

Propiedades de la Radicación (tabla 2)

Gracias a las propiedades anteriores podemos desarrollar ejercicios de simplificación que tomarán importancia en cálculos posteriores al enfrentarnos a definiciones más complejas.

Multiplicaciones de expresiones Radicales con igual indice

Si observamos la primer propiedad de la tabla 2 llamada "producto de radicales del mismo indice" nos damos cuenta que la operación de multiplicación, se realiza entre los radicandos, conservando la misma raiz (mismo indice). Veamos algunos ejemplos:

Otro ejemplo:

Para complementar vamos a ver un video sobre la multiplicación de expresiones radicales. Recuerda debes estar tomando apuntes en tu cuaderno como evidencia académica y para poder repasar luego.

Video 1: Multiplicación de Expresiones Radicales de igual indice

Video 2: Otro ejemplo

Actividad Evaluativa 2

Para esta semana debes desarrollar el siguiente taller en tu cuaderno y tomarle foto o escanear (puedes descargar un app de escáner en tu celular así los archivos pesan menos y puedes cargarlos con mayor facilidad) debes enviar todas las fotos con el procedimiento y los resultados al correo electrónico profeagl@gmail.com debidamente marcado con nombres y apellidos completos

IMPORTANTE: no se reciben actividades por whatsApp, solo pueden ser enviados por correo electrónico a la dirección que se dijo anteriormente.

______________________________________________________

Semana 1 y 2 (del 20 al 30 de abril de 2020)

Recordemos lo estudiado hasta el momento

Durante las anteriores clases, hemos realizado un repaso sobre las operaciones de reducción de términos (adición) y la multiplicación entre polinomios algebraicos. Posteriormente centramos la atención en la radicación en números reales y sus propiedades, inicialmente en la reducción de términos semejantes que contienen radicales. Para continuar nuestro estudio alrededor de la radicación, es importante fortalecer lo aprendido, por eso encontrarás un vídeo y ejemplos que te permitirán repasar y seguidamente resolver la actividad 1. 

Vídeo 1: Reducción de términos semejantes en un polinomio (Repaso)

Video 2: Suma y resta de expresiones radicales

Espero estos vídeos te hayan servido para recordar aquello que hemos estudiado en clases, ahora vamos a resolver nuestra primer actividad.

Actividad 1a: completa la siguiente prueba corta

Actividad 1b: Práctica para verificar tratamientos matemáticos correctos. (haz clic sobre la imagen)

Para tener en cuenta: todos los tratamientos matemáticos realizados para resolver cada ejercicio, deben quedar escritos en tu cuaderno de álgebra como evidencia del trabajo realizado.