Geometría 9° (2 y 3)

Semana 11-13 (del 30 de junio al 17 de julio de 2020)

finalización de Semestre

Teorema de Thales (o Tales)

Hola chicos espero se encuentren muy bien, ya estamos en la recta final de este primer semestre del año escolar y ha sido todo un reto de aprendizaje, los felicito por todo su esfuerzo y responsabilidad. Vamos a cerrar nuestro semestre dando continuidad al tema de semejanza entre triángulos, recuerda que las semanas anteriores trabajamos con los criterios de semejanza. Como nota recordatoria tenemos:

Dos triángulos son semejantes entre sí, si conservan la misma forma (lados proporcionales) y sus ángulos son congruentes. Podemos verificar si dos triángulos son semejantes usando tres criterios que son:

LAL (Lado, ángulo, lado): si dos lados son proporcionales y el ángulo comprendido entre ellos es congruente.

LLL (lado, lado, lado): si los tres lados de los dos triángulos son proporcionales.

AA (Ángulo, ángulo): si dos de los tres ángulos de los triángulos son congruentes.

Te invito a repasar la clase anterior y revisar la actividad que realizaste.

Continuemos, el teorema de Tales establece una relación de proporcionalidad entre los segmentos que se forman al cortar dos o más rectas paralelas con otras rectas transversales (rectas secantes) como se observa en la figura:

El teorema establece los siguiente:

Gracias a este teorema, podemos encontrar el valor desconocido de segmentos cuya disposición cumpla con el teorema. Por ejemplo:

como puedes observar, a través de este teorema y del manejo de proporciones y ecuaciones, podemos encontrar el valor de la medida de los segmentos. Veamos más ejemplos:

A continuación se presentan un grupo de videos como apoyo a este tema, después debes desarrollar la actividad propuesta en tu cuaderno y enviarla al correo electrónico profeagl@gmail.com tienes plazo hasta el 17 de julio de entregar y/o realizar todas las actividades que tengas pendientes de geometría, en esta fecha cierra el periodo. 

Video 1:

Video 2:

Video 3:

Actividad Evaluativa

Desarrolla cada ejercicio y problema en tu cuaderno, toma foto o escanea y envía por correo.

________________________________________________________________

Semana 7-10 (del 1 al 26 de junio de 2020)

Semejanza de triángulos

Hola chicos, espero que se encuentren muy bien. Vamos a iniciar la clase correspondiente a las semanas 7 y 8, nuestro tema de estudio es la semejanza de triángulos. Hasta el momento ustedes han tenido la oportunidad de trabajar con la congruencia de triángulos, recordemos que congruencia hace referencia a la misma forma e igual medida, es decir, que si dos figuras geométricas son congruentes, son idénticas, aunque suposición en el plano o el espacio cambie, su forma y medida no cambian. 

En el caso de la semejanza uno de los criterios no se mantiene. la semejanza de triángulos conserva la forma y la medida de los ángulos de las figuras semejantes, pero su tamaño no. Por ejemplo, si pensamos en una maqueta que este a escala (esto significa que existe una proporción entre las medidas) es una representación disminuida de lo que será la construcción en tamaño real; otro ejemplo son las fotografías, aunque su tamaño no corresponda a nuestras medidas reales, son una representación disminuida que respeta las proporciones.

Hemos mencionado mucho la palabra proporción, recuerda que una proporción es la igualdad entre dos razones, o dicho de otra forma, dos medidas son proporcionales si podemos expresar una como múltiplo o submúltiplo de la otra.

Para que dos figuras, en este caso, dos triángulos sean semejantes, deben cumplirse dos condiciones:

1. Sus ángulos deben ser congruentes (medir lo mismo)
2. La medida de sus lados deben ser proporcionales

Por ejemplo, observa los siguientes triángulos:

Aunque los dos triángulos no tienen el mismo tamaño, si medimos sus ángulos podemos comprobar que son iguales, además al establecer la razón entre sus lados correspondientes se encontrara el mismo valor, lo que significa que sus tres lados son proporcionales:

4,18/2,2= 1,9

6,65/3,5= 1,9

7,6/ 4= 1,9

Vemos que se cumplen las dos condiciones de semejanza: ángulos congruentes y lados proporcionales.

Como no siempre se cuenta con tanta información, podemos utilizar tres criterios de semejanza entre triángulos:

Criterio de semejanza 1:

Si dos triángulos tienen dos ángulos congruentes, entonces son semejantes (AA)

Criterio de semejanza 2:

Si dos triángulos tienen dos lados proporcionales (igual razón) y el ángulo que se encuentra entre ellos es congruente, entonces los triángulos son semejantes (LAL)

Criterio de semejanza 3:

Si dos triángulos tiene sus tres lados proporcionales (igual razón), entonces los triángulos son semejantes (LLL)

Observemos los siguientes ejemplos:

Otro ejemplo

Un ejemplo más

Ahora vamos a complementar la clase con algunos videos que te ayudarán a entender mejor este tema de estudio, recuerda tomar nota en tu cuaderno de lo teórico y algunos ejemplos, que te sirvan como evidencia académica y para repasar constantemente.

Video 1

Video 2

Video 3

Video 4

Video 5

Actividad Evaluativa Semana 7-8

Espero que tanto las explicaciones de la clase como la de los videos te permitan resolver la siguiente actividad. Recuerda dar clic en enviar al final y llegará a mi correo automáticamente. Esta vez NO tienes que enviar nada a parte en fotos, solo este cuestionario desde aqui mismo.

-----------------------------------------------------------------------------------------

Semana 5-6 (del 18 al 29 de mayo de 2020)

Ángulos formados entre rectas o segmentos paralelos cortados por una transversal

Hola a todos, espero se encuentren muy bien y con toda la disposición para iniciar la clase y actividades de la semana 5 y 6, teniendo en cuenta la densidad de actividades que tienen de todas las asignaturas, de esta manera tendrás más tiempo para su desarrollo. 

Vamos a trabajar un tipo especial de ángulos, estos tienen características únicas debido a su construcción, ya que se forman entre rectas paralelas (recuerden que este tipo de rectas o segmentos son aquellos que no se interceptan y siempre mantienen la misma distancia entre ellos). Cuando un par de rectas (o segmentos) paralelos son cortados por una recta (o segmento) transversal, se forman ángulos cuyas medidas guardan propiedades específicas.

Recuerda tomar nota en tu cuaderno de cada concepto como evidencia de la actividad académica y para que puedas repasar en el futuro. 

Vamos a clasificar cada tipo de ángulo:

Ángulos Opuestos por el vértice: conocidos también como ángulos verticales, y son aquellos que se forman con las misma rectas y comparten en común el vértice. Los ángulos opuestos por el vértice son CONGRUENTES.

Vídeo 1: Ángulos Opuestos por el Vértice

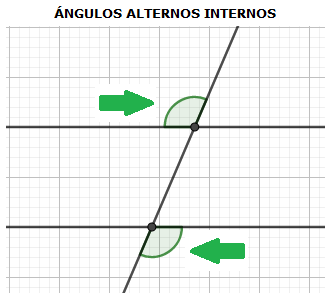
Ángulos Alternos Internos: son aquellos ángulos formados al interior de las rectas o segmentos paralelos y la transversal, pero a lado contrario de la transversal sin compartir lado en común. Los ángulos alternos internos son CONGRUENTES.

Vídeo 2: Ángulos Alternos Internos

Ángulos Alternos Externos: son aquellos ángulos formados en el exterior de las rectas o segmentos paralelos y la transversal, pero a lado contrario de la trasversal sin compartir lado en común. Los ángulos alternos externos son CONGRUENTES.

Vídeo 3: Ángulos Externos

Ángulos Suplementarios: son aquellos ángulos que al unirse forman un ángulo llano, es decir que la suma de sus medidas siempre es 180°. Los ángulos suplementarios SIEMPRE SUMAN 180°.

Vídeo 4: Ángulos Suplementarios

Ángulos Correspondientes: Son aquellos ángulos que se encuentran al mismo lado de la recta o segmento transversal, siendo uno interno y el otro externo. Los ángulos correspondientes son CONGRUENTES.

Vídeo 5: Ángulos Correspondientes

Vídeo final: Ángulos entre paralelas y transversales

ACTIVIDAD EVALUATIVA 3

________________________________________________________________

Semana 3 y 4 (del 4 al 15 de mayo de 2020)

Teoremas sobre las rectas notables de un triángulo

Hola, espero que estés súper bien y cuidándote en casita, además listo para iniciar de nuevo nuestras actividades académicas luego de este forzoso receso. Vamos a continuar con el proceso de aprendizaje sobre las rectas notables que podemos trazar en un triángulo que son las medianas, las mediatrices, las bisectrices y las alturas (recuerda que lo puedes repasar en la semana 1).

Para continuar con nuestro proceso de aprendizaje, esta semana vamos a explorar algunos teoremas que involucran dichas rectas, y como podemos usarlos en la resolución de problemas. Para iniciar, necesito que tengas a la mano tu cuaderno para tomar apunte de todos los teoremas y tus instrumentos de construcción geométrica (regla, escuadras, compás y transportador). Además, si tienes la posibilidad de descargar en tu computador, tablet o celular el program de Geogebra (gratuito) será un apoyo en la exploración de las características y propiedades de las rectas notables estudiadas. Ahora si, comencemos.

Observa que en la figura 1, para el triángulo ABC, se construye las rectas mediatrices (ver clase semana 1), las cuales se intersecan en el punto O que se convierte en el centro de la circunferencia. En este caso donde la circunferencia contiene a todos los vértices del triángulo, decimos que el triángulo está circunscrito.De acuerdo al teorema (T1), ¿cómo son las medidas de los segmentos AO, BO, CO?

Conocer este teorema permite la resolución de algunos enunciados problemas como:

Se quiere construir una estación del tren, de tal manera que este a la misma distancia del pueblo Arcos, del pueblo Búfalo y del pueblo Cisnes. Demuestra geométricamente el lugar donde debe construirse la estación.

Video 1: solución al problema anterior

Otro propiedad que tienen las rectas medianas en un triángulo, es que subdivide al triángulo en seis partes de igual área.

Estos tres teoremas son importantes para complementar las propiedades de los triángulos. Ahora podemos resolver la actividad de la semana 2. Recuerda copiar en tu cuaderno los 3 teoremas vistos esta semana como evidencia académica y como apoyo de estudio en casa.

Actividad Evaluativa 2

___________________________________________________________________

Semana 1 y 2 (del 20 al 30 de abril de 2020)

Repasar y profundizar en el estudio de las rectas notables de un triángulo. 

Vamos a repasar las definiciones de las rectas notables de un triángulo que estuvimos estudiando en clases.

Recordemos:

Vídeo 1: Rectas notables de un triángulo

Vídeo 2: Mediana, mediatriz, bisectriz y alturas de un triángulo

Vídeo 3: Construcción

En la siguiente figura podemos ver en resumen cada tipo de recta notable de un triángulo y su punto de intersección:

Actividad 1

Resuelve el siguiente cuestionario, apoyándote en lo estudiado en clases y los recursos anteriores, al finalizar dar clic en enviar.