Semana 10-13 (del 1 al 17 de julio de 2020)
Finalización de semestre (periodo 1)
Representaciones de un número racional
Hola chicos, espero se encuentren muy bien. Ya iniciamos la recta final de este primer periodo (semestre) que ha sido tan dificil en medio de la emergencia de salud que vivimos en todo el mundo, pero por tu responsabilidad y dedicación podemos lograr terminar con éxito esta primer etapa.
En esta última clase del periodo vamos a ver las diferentes formas de representar un mismo número, recuerda que en matemáticas trabajamos con representaciones de los objetos matemáticos com los números. En esta ocasión nuestra atención se centra en las formas de representar un número fraccionario, son seis las representaciones que exploraremos y veremos como cambiar de una representación a otra, así podremos reconocer el mismo número en formas diferentes.
Primero recordemos que el número fraccionario representa una parte de la unidad, donde tenemos un número de partes igua1les (partición) en las que la unidad entera se divide, para luego poder tomar de ella lo necesario.
Además, recordemos que una unidad entera puede representarse por una fracción cuando el número de particiones es igual al número de partes que tomamos, por ejemplo, 1 unidad entera puede escribirse como 5/5 (cinco quintos) que significa que la unidad se divide en cinco partes iguales y las usamos todas, es decir, tomamos las cinco. Otro ejemplo de unidad entera es 8/8, que significa que la unidad se divide en ocho partes iguales y se usan todas.
Ahora después de este breve repaso, vamos a mirar las seis formas diferentes de representar un mismo número:
1) REPRESENTACIÓN NUMÉRICA FRACCIONARIA: Esta forma es la que estamos trabajando, la escritura fraccionaria consta de una partición (denominador) y el número que representa la parte que tomamos (numerador), ambos número son enteros y se relacionan como un cociente (división) usando el símbolo "/", por ejemplo, son representaciones fraccionarias las siguientes:
2) REPRESENTACIÓN DISCURSIVA (escritura en palabras): es la forma en palabras que toma el número fraccionario. En el ejemplo anterior aparece la forma como se nombra y escribe cada representación numérica fraccionaria.
3) REPRESENTACIÓN NUMÉRICA MIXTA: Un número mixto es la combinación de un número entero con un número fraccionario. Para convertir una representación numérica fraccionaria en una representación numérica mixta, debemos calcular cuantas unidades enteras se pueden formar a partir de la fracción dada, es decir, cuantos grupos iguales a la partición se pueden formar. Por ejemplo,
en el primer caso, tenemos ocho quintos (8/5), que esta representado en forma fraccionaria, podemos observar que la partición es cinco, es decir, una unidad entera se divide en cinco partes iguales, pero necesitamos 8 partes, así que alcanzamos a formar una unidad entera (5/5) y aún faltan 3 partes, o sea tres quintos (3/5), de esta manera podemos escribir 8/5 como 1 unidad entera con 3/5. También puedes utilizar la división preguntandote ¿cuántas veces cabe el 5 (la partición) en el 8? la respuesta es cabe una (1) vez y sobran 3 partes (tres quintos).
en el segundo caso, tenemos veinte tercios (20/3), que esta representado en forma fraccionaria, podemos observar que la partición es tres, es decir, una unidad entera se divide en tres partes iguales, pero necesitamos 20 partes, así que alcanzamos a formar seis unidades enteras (18/3 = 18 dividido entre 30 6) y aún faltan 2 partes, o sea dos tercios (2/3), de esta manera podemos escribir 20/3 como 6 unidades enteras con 2/3. También puedes utilizar la división preguntandote ¿cuántas veces cabe el 3 (la partición) en el 20? la respuesta es cabe seis (6) veces y sobran 2 partes (dos tercios).
Para convertir un número fraccionario en un número decimal con coma, debemos dividir los números enteros que forman la fracción (numerador entre denominador): si tenemos 64/5 podemos dividir 64 entre 5 para obtener el número decimal con coma (esto pasa cuando la división no es exacta)
En la recta numérica también se ubican los números fraccionarios. Recuerda que la partición (denominador) nos indica en cuantas partes iguales se debe dividir la unidad (cada unidad entera se divide en las mismas particiones) para luego seleccionar las partes que indica el numerador. Por ejemplo, en la fracción 2/5 la partición (5) nos indica que la unidad entera (iniciando desde cero) debe dividirse en cinco partes iguales, y luego debemos tomar dos de esas partes, es decir, dos quintos (cada parte dividida representa un quinto )
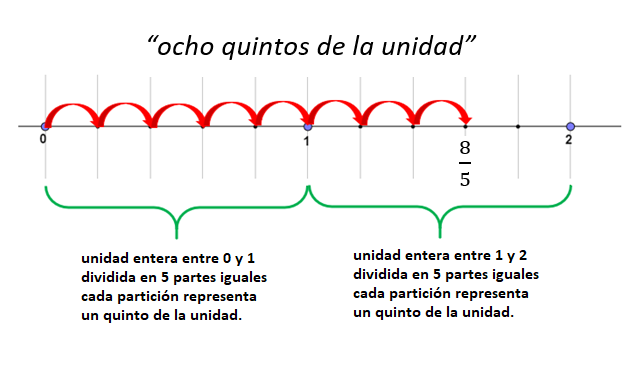
Otro ejemplo, el número fraccionario 8/5, nos indica que la unidad entera debe dividirse en 5 partes iguales (porque la partición es 5), para luego tomar 8 partes. Pero como con la primer unidad no es suficiente, debemos tomar la siguiente unidad (entre 1 y 2) volver a dividirla, en esta ocasión alcanzamos a completar las 8 partes que necesitamos:
6) REPRESENTACIÓN BIDIMENSIONAL (FIGURAS PLANAS): Finalmente, todo número fraccionario puede representarse a partir de figuras como las geométricas, donde representemos la partición para dividir la unidad en partes iguales y luego, usando color o sombreado, representemos las partes tomadas:
Muy bien, con lo que hemos expuesto podemos enfrentarnos a la actividad de evaluación, recuerda tomar apuntes en tu cuaderno de esta clase, es muy importante tenerlo en tu cuaderno para repasar constantemente.
Para desarrollar la actividad utiliza el siguiente ejemplo como guía:
Ejemplo: Representa en las seis maneras estudiadas, cada número fraccionario dado
ACTIVIDAD EVALUATIVA
Completa la siguiente tabla, a partir de los dos números fraccionarios dados. Copia en tu cuaderno, toma foto o escanea y envía al correo electrónico profeagl@gmail.com
Semana 7-9 (del 16 al 30 de junio de 2020)
FRACCIONES EQUIVALENTES
AMPLIFICACIÓN Y HOMOGENEIZACIÓN
Hola chicos, espero se encuentren muy bien, esta dos semanas vamos a retomar el trabajo con los números fraccionarios en sus diferentes representaciones. Recuerda que podemos representarlos numéricamente como fracciones, como decimales (dividiendo) o de forma bidimensional (figuras poligonales). En la última clase sobre fracciones (revisa semana 3 y 4) aprendimos sobre las fracciones, sus características y como podemos representarlas, te invito a repasar esa clase para poder continuar con su estudio.
En estas semanas vamos a trabajar con dos operaciones muy importantes y útiles a la hora de estudiar las fracciones, estas operaciones son la amplificación y la homogeneización.
Empecemos con la primera. Para amplificar vamos a usar la multiplicación, en este caso voy a emplear el símbolo asterisco (*) para multiplicar. Ahora sí manos a la obra:
Tenemos un nuevo concepto por definir, las fracciones equivalentes, que son aquellas que aunque se escriben con valores diferentes, representan la misma relación parte- todo. Siempre podemos obtener fracciones equivalente usando la amplificación. Veamos más ejemplos:
Muy bien, ahora estamos listos para hacer el punto 1 de nuestra actividad de la semana. Pero antes veamos la otra operación importante, la homogeneización:
Muy bien, la homogeneización es una operación que nos permite comparar. Veamos algunos videos que seguramente te ayudarán a entender mejor lo visto en esta clase:
Video 1
Video 2
ACTIVIDAD SEMANA 7-8
Debes desarrollar la actividad en tu cuaderno, y luego tomar foto o escanear para enviar al correo profeagl@gmail.com . RECUERDA MARCAR TU CORREO CON NOMBRE COMPLETO Y GRUPO, ES MUY IMPORTANTE PARA PODER REVISAR.
-----------------------------------------------------------------------------------------
Semana 5-6 (del 18 al 29 de mayo de 2020)
Conceptos de Geometría: Figuras planas y Cuerpos geométricos
Hola a todos, teniendo en cuenta la densidad de clases y actividades presentadas en todas las asignaturas y a petición de padres y estudiantes, las actividades de aprendizaje se publicarán para dos semanas, así tendrás más tiempo para su estudio y desarrollo.
Durante la semana 5 y 6, centraremos nuestra clase en geometría, específicamente en el repaso de las figuras planas y las características de los cuerpo o sólidos geométricos, principalmente los llamados prismas y pirámides.
Ya hemos trabajado en grados y clases anteriores, algunas características de las figuras planas, como su forma (limitada por segmentos rectos o líneas curvas) lo que nos permite clasificarla como figuras poligonales (o solo polígonos) o figuras curvilíneas (como el círculo).
Figuras Curvilíneas: son aquellas figuras planas cerradas limitadas por una línea continúa (no tiene lados) el ejemplo más conocido es el círculo y el ovalo.
Polígonos: Son figuras planas cerrada limitadas por segmentos de recta que se unen en los vértices, marcados como puntos de intersección entre los lados del polígono. Entre cada par de lados consecutivos se forman ángulos. Es decir, que un polígono es una figura plana formada por lados, vértices y ángulos.
Los polígonos se clasifican según el número de lados:
3 lados, 3 vértices y 3 ángulos se llaman triángulos
4 lados, 4 vértices y 4 ángulos se llaman cuadriláteros
5 lados, 5 vértices y 5 ángulos se llaman pentágonos
(consulta y copia en tu cuaderno como se llaman los polígonos de 6, 7, 8, 9, 10, 12, 20 lados)
Cuando vemos una figura plana como un polígono, decimos que es una figura bidimensional (dos dimensiones) porque tiene largo y ancho (o largo y alto).
Cuando vemos la representación de un cuerpo geométrico, como el cubo (piensa en un dado) decimos que es una figura tridimensional ya que se forma en tres dimensiones (largo, ancho y alto o profundidad), los cuerpos tridimensionales pueden ser físicos como el mundo que nos rodea (incluso nosotros mismos) pero cuando tratamos de construir en una hoja o en una pantalla un cuerpo tridimensional, realmente estamos usando la perspectiva para representar la tercera dimensión como por ejemplo lo que hacen con las películas del cine en 3D.
Son ejemplos de representaciones de figuras tridimensionales los siguientes:
Como podemos observar, en un sólido geométricos podemos identificar figuras planas como los polígonos. En estos casos el sólido recibe el nombre de poliedros.
Todos los poliedros tiene las siguientes características:
- Vértices: representados por los puntos donde se intersecan (se encuentran) tres lados a la vez.
- Arista: es el segmento de recta donde se encuentran dos lados de los polígonos que forman el poliedro.
- Caras bases y caras laterales: son los polígonos que le dan forma al poliedro.
- Ángulos internos del poliedro: formados entre cada par de caras.
Los poliedros se clasifican en dos grupos importantes: Los primas y las pirámides.
Los primas: Sólidos geométricos formados por polígonos que tienen las siguientes características:
- Tiene dos caras bases que son paralelas entre sí (es decir que están separadas la mism distancia en cualquier punto sobre ellas) y estas caras bases puede ser cualquier polígono.
- Tiene caras laterales formadas SIEMPRE por rectángulos (recuerda que un cuadrado también es un rectángulo).
- Si entre la cara lateral y la cara base se forma un ángulo recto, decimos que el prisma es recto, de lo contrario el prisma es oblicuo.
Las pirámides: son sólidos geométricos formados por polígonos que tienen las siguientes características:
- Tiene una sola cara base que puede ser cualquier polígono.
- Tiene caras laterales formadas solo por triángulos.
- Tiene una cúspide (es el vértice donde se intersectan todas las caras laterales)
No debemos confundir una figura plana (bidimensional) con una figura tridimensional.
Recuerda copiar en tu cuaderno lo más importante para tener como evidencia de actividad académica y para que puedas repasar constantemente.
Observa los siguientes vídeos para fortalecer lo que se expuso anteriormente:
Vídeo 1: Repaso de polígonos
Vídeo 2: Aprender sobre sólidos geométricos
Vídeo 3: Más sobre sólidos geométricos
________________________________________________________________
Semana 3 y 4 (del 4 al 15 de mayo de 2020):
Los números Fraccionarios
Hola, espero que estés súper bien y cuidándote en casita, además listo para iniciar de nuevo nuestras actividades académicas luego de este forzoso receso. Vamos a continuar con el proceso de aprendizaje de matemáticas, ya hemos realizado un trabajo de repaso sobre los números enteros (aquellos números que representan unidades exactas ya sean positivas o negativas), ahora vamos a comenzar a reconocer las características de un nuevo conjunto numérico llamado el conjunto de los números Racionales (Q).
Sin embargo, es muy importante para el aprendizaje de este conjunto numérico, hacer un trabajo académico previo sobre los números fraccionarios, aquellos que se escriben numéricamente como:
Los números fraccionarios se usan para representar partes de una unidad entera, por ejemplo cuando tenemos una unidad entera y la subdividimos en partes iguales cuya suma forman de nuevo la unidad:
Cada subdivisión tiene el mismo tamaño, es decir que las partes son congruentes. Podemos representar las partes de la unidad con la escritura numérica fraccionaria y designarla con la escritura en palabras:
Las partes en que se divide la unidad recibe el nombre de partición, también la llaman denominador, y las que representan una parte del total se les llama numerador en su escritura numérica fraccionaria.
En la figura anterior, la unidad entera se ha subdivido en seis partes congruentes (igual medida de superficie), este valor representa la partición de la unidad y se le llama denominador, la parte sombreada de color verde es una parte de la totalidad y se le llama numerador.
Los números fraccionarios pueden representarse en diferentes formas: representación numérica fraccionaria, representación bidimensional (figura plana), representación unidimensional (punto sobre la recta numérica), representación numérica mixta (combinación de unidades enteras con fraccionarias), representación decimal no entera (número decimal con coma).
Para terminar esta introducción al estudio de las fracciones, vamos a observar el siguiente video:
video 1: Representación numérica fraccionaria
Antes de desarrollar la actividad evaluativa de la semana 2, vamos a practicar un poco sobre lo aprendido hasta ahora. Haz clic sobre cada imagen (en total son 2 actividades interactivas)
1
2
Uff!!!! después de tanta práctica podemos realizar la actividad evaluativa de la semana. Manos a la obra
ACTIVIDAD EVALUATIVA 2
___________________________________________________________________________
Semana 1 y 2 (del 20 al 30 de abril de 2020)
Recordemos lo aprendido
A continuación se presenta un enlace que te redireccionará hacía un libro digital donde podrás repasar temas relacionados con los números enteros, observar ejemplos, practicar y profundizar sobre las operaciones y relaciones entre los elementos de este conjunto numérico. Explora y práctica.
(dar clic a la imagen)
No hay comentarios:
Publicar un comentario